Basic principle If you want to gain confidence in the field of mathematics, you should begin with the fundamentals. Just as a tall building requires a strong foundation, mastering the fundamentals of mathematics is critical. Multiplication is one such operation with numerous ramifications. It has a wide range of applications and is available in a variety of forms. The level of multiplication increases as we progress through the grades. We begin with the fundamentals of multiplication between two simple numbers of Basic principle. We are informed that the obtained product can be completely divided by the two numbers from which it is obtained. We are introduced to the multiplication of algebraic equations in higher-level classes. As we progress through higher-level mathematics, we become more familiar with the product of two functions. This variation elucidates the beauty of mathematics of Basic principle. lcm is one of the most important applications of multiplication. Lcm is an abbreviation for lowest common multiple, which denotes the smallest multiple of the given numbers. This has severa applications. It is useful in the addition and subtraction of fractions. Lcm has numerous other important applications. For example, knowing the dimensions of a box allows us to calculate how much paper will be needed to cover it. This is a classic example of the significance of lcm. The numbers with the lowest common multiple are factors to it. In this section, we will go over the concept and properties of the lowest common multiple in-depth.
The Fundamentals of lcm and Basic principle
Table of Contents
Applications: Lcm is important in the chapter fractions. It can be used to compute the sum and difference of two simple fractions. It is also useful for comparing a large number of fractions. These factors explain why lcm is required. It is also very useful in resolving all problems involving machine meshing gears. It is used to calculate the number of rotations required for realignment of Basic principle. This is accomplished by calculating the lcm of the teeth of the respective gears. The application of lcm solves all problems relating to mesh gears. Similarly, the concept of lcm can be useful in resolving problems involving planet alignment. These elements represent the importance of lcm.
Calculation:
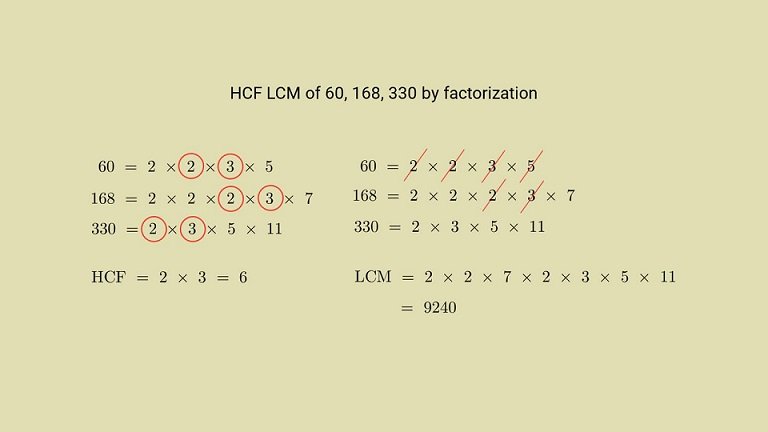
The time-consuming process of calculating the lcm is to create a table of the given numbers and look for the first product that is shared by all of them. When a common product is discovered, that product becomes the lcm. However, this method is time-consuming and should only be used for small numbers. Using prime numbers, we can illustrate the concept of factorization. The given numbers from which the lcm is to be calculated can be represented as powers of prime numbers. The lcm is the sum of all prime numbers raised to their highest powers of Basic principle. This method is extremely effective for determining the lcm. The table method is the most efficient way to obtain the lcm. Tables are used to store the numbers for which the lcm is to be calculated. The division by prime numbers is then begun. When prime numbers are the only remaining constituents in the table, the product yields the lcm.
This is without a doubt the most efficient method of calculating the lcm. Using this method, determining the lcm of multiple numbers is a breeze.
All of the major concepts and calculations associated with lcm have been thoroughly discussed here. This is a critical application of multiplication that is tested in both lower and upper grades. This topic is also covered in several competitive exams. This implies that students must pay close attention to this critical subject. Cuemath, an online platform for all math and coding-related questions, may be of assistance. Teachers also use this platform to improve their teaching methods. We hope that this article has helped broaden your understanding of lcm.